Lab 3: Non-constant acceleration problem/activity

Problem with a Non-constant Acceleration

Jin Im

6 March, 2017

In this lab, we explored how to solve, with Microsoft Excel, a kinematic equation in which the acceleration component was not constant -- normal kinematics equations do not apply. 

Introduction: A 5000 kg elephant on frictionless roller skates is going 15 m/s when it gets to the bottom of a hill and arrives on level ground. At that point a 1500 kg rocket mounted on the elephants back generates a constant 8000 N thrust opposite the elephant's direction of motion. The mass of the rocket changes with time (due to burning the fuel at a rate of 20 kg/s) so that the m(t) = 1500kg - 20kg/s*t. Find how far the elephant moves before coming to rest. 

We are given the analytical solution to this problem in the lab manual beforehand:

The answer to our problem is 248.7 meters. However, the process was very difficult and involved. The alternative way of solving this problem involves the use of Microsoft Excel, and is much faster.

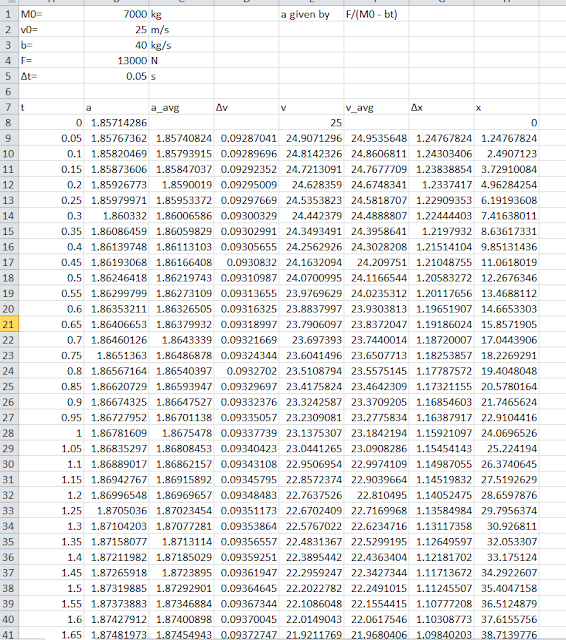
Procedure: 

On our excel page, we attributed cells with static values including ∆t, initial mass, force, initial velocity, and fuel burn rate. We then created a row for dynamic values of elapsed time, acceleration, average(mid-point) acceleration, ∆v, velocity, average(mid-point) velocity, ∆x, and x. We set up these cells so they update with every row and time interval. 

Time was the previous value of time + ∆t.

Acceleration was the Force divided by the quantity for (Mass - burnrate*time).

Average acceleration was the mean of the accelerations at the beginning and the end of each time interval

∆v was average acceleration*∆t

Velocity was initially 25 m/s and reduced by ∆v for every time interval

Average velocity is the mean of the velocities in the beginning and end of each time interval

∆x is average velocity*∆t

x is the sum of all ∆x's.

The result is a spreadsheet like such:

Because we are interested in how far the elephant travels before coming to a stop, we can look at the t in which the velocity hits zero. From this, we can conclude from this data that the elephant stops moving by virtue of its initial motion between 19 and 20 seconds, and starts to move backwards due to the rocket, shown by the velocity becoming negative. Manipulating our value for ∆t can give us more precise results by giving us data in smaller increments of time. For example, changing ∆t from 1 to 0.05 shows that the time at which the elephant stops moving is closer to 19.7 seconds.

Conclusions: 

A problem with multiple integrals was solved within microsoft excel in under an hour. By using cell references and simple formulas, we are able to learn that the elephant travels 248.7 meters, which is the same total distance solved in the analytical approach. By manipulating the value of ∆t until our final velocity is as close as we want, we are able to get accurate results. By changing the values in our static cell references, we are able to solve similar problems with much less effort. For example,  if the elephant's mass was instead 5500 kg, the fuel burn rate is 40 kg/s, and thrust force was 13000 N, we would be able to find that the distance the elephant is able to travel is around 164.0 meters.